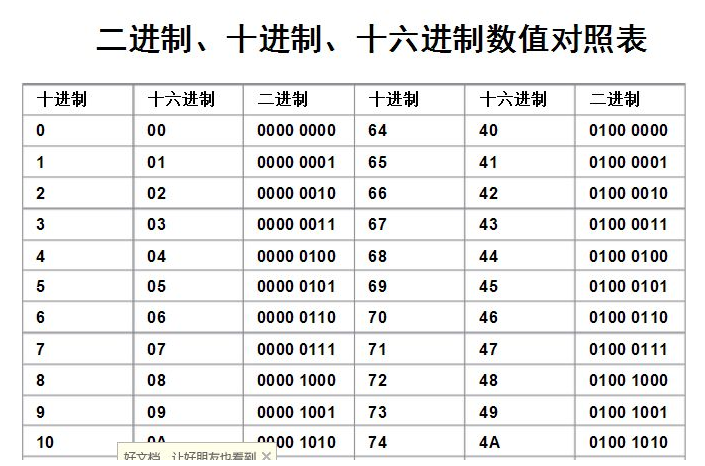
Hexadecimal (English name: Hexadecimal) is a representation of data in a computer. It is different from the representation in our daily life. It consists of 0-9, AF, and the letters are not case sensitive. The correspondence with the decimal is: 0-9 corresponds to 0-9; AF corresponds to 10-15; N-digit numbers can be represented by numbers of 0~(N-1), and letters AF exceeding 9 are used.
1, BCD code and decimal number conversion
The conversion relationship between BCD code and decimal number is very intuitive, and the mutual conversion is also very simple. Convert the decimal number 75.4 to BCD code: 7-"0111,5-"0101,4-"0100, so the result of spelling 8421BCD code is:( 0111 0101.0100) BCD; if the BCD code 1000 0101.0101 is converted to a decimal number: 1000-"8,0101-"5,0101-"5, the result is: (85.5)D.
Note: The number represented by the same 8-bit binary code is not the same when it is considered to represent a binary number and it is considered to be a binary-coded decimal number.
For example, when it is treated as a binary number, its value is 24; but as a 2-bit BCD code, its value is 18.
Also for example, 00011100, if it is treated as a binary number, its value is 28, but it cannot be regarded as a BCD code because it is an illegal code in the 8421 BCD code.
2, BCD code format
The BCD code in the computer is often used in two formats, namely, separating the BCD code and combining the BCD code.
The so-called split BCD code, that is, a one-byte low-digit code represents a digit of a decimal number, for example, the storage format of the number 82 is:
_ _ _1 0 0 0 _ _ _ _0 _0 0 1 0 where _ indicates an irrelevant value.
Combine the BCD code, store the two decimal numbers in one byte, and the storage format of the example 82 is 1000 0010.
3. Addition and subtraction of BCD code
Since the encoding is to represent each decimal number with a set of 4-bit binary numbers, if you pass this BCD code directly to the computer, because
Computers always treat numbers as binary numbers, so the results can go wrong. Example: Use the BCD code to find 38+49.
The solution is to use the "plus 6 correction" for the result of the binary addition. This correction is called BCD adjustment. The result of the binary addition is corrected to the result of the BCD code addition. When the two two-bit BCD numbers are added, The result of the binary addition is corrected by the correction rule. The correction rule:
(1) If the result of adding any two corresponding bit BCD numbers is higher than one bit, if the result is less than or equal to 9, the bit does not need to be corrected; if the result is greater than 9 and less than 16, the Bits are added with 6 corrections.
(2) If the result of adding any two corresponding bit BCD numbers has a carry to the upper bit (ie, the result is greater than or equal to 16, note that the carry is not the correction), the bit is corrected by 6.
(3) When the low position correction result is such that the high level is greater than 9, the high position is added with 6 corrections.
The following example verifies the correctness of the above rules.
a) Use the BCD code to find 35+21
35-》 0011 0101+
21-》 0010 0001=
0101 0110-"56
Note: 0101+0001 does not satisfy the above three rules, and 0011+0010 does not satisfy the above three rules, so the result is not processed.
b) BCD code for 25+37
25-》0010 0101+
37-》0011 0111=
0101 1100+ (lower 0101+0111=1100-"12"9 so adjustment is required)
06-》 0110=
0110 0010-"62
Note: There is also a carry to the high position when adding the 0110 adjustment to the low position, but this is the carry at the time of adjustment, so no processing is done.
c) Use the BCD code to find 38+49
38-》0011 1000+
49-》01001001=
1000 0001+ (there is a carry when the low 1000+1001 is added, so you need to add the 0110- to the lower digit)
06-》 0110=
10000111-"87
Note that the adjusted result does not satisfy the above condition (3), so it is no longer adjusted.
d) Use the BCD code to find 42+95
42-》0100 0010+
95-"1001 0101=
11010111-"13 7+(1101 is an illegal 8421BCD code, and 0100+1001 is added to meet the condition of (1))
06-"0110 (note that it is adjusted for 1001+0100 plus 0110)
00010011 0111-"1 3 7
Note that the result does not satisfy the (3) condition and is therefore not adjusted.
c) Use the BCD code to find 91+83
91-"1001 0001+
83-"1000 0011=
00010001 0100 +(1001+1000 has a carry, so you need to add 1001+1000 to add 0001+0110)
06-》0110 =
00010111 0100-》174
Note that the result does not satisfy the (3) condition and is therefore not adjusted.
d) Use the BCD code to find 94+7
94-"1001 0100+
07-"0000 0111=
10011011+ (Because the result of the two-digit code number satisfies the above condition 1, it needs to be adjusted to 0100+0111+0110)
06-》0110=
1010 0001+ (since the high level of the result 1010-"10"9, the above condition (3) is satisfied and the high position is adjusted by 0110)
06-》0110 =
0001 0000 0001-"101
Note: For the adjustment we only need to care whether the result meets the above condition (3) and does not satisfy the adjustment.
e) Use the BCD code to find 76+45
76-》0111 0110+
45-》0100 0101=
1011 1011+ (Note that 0101+1011 and 0111+0100 both satisfy the above condition (1), so they need to be adjusted)
06-》01100110=
000100100001-"121
Note that the result satisfies the above condition (3) and is therefore not adjusted. (example added in 2015-1-11)
When the two combined BCD codes are subtracted, when there is a borrow from the low position to the high position, the difference between the "borrow one for sixteen" and "borrow one for ten" will be 6 more than the correct result, so when there is a borrow, Use the "minus 6 correction method" to correct. When two BCD codes are added or subtracted, the binary addition and subtraction instructions are first used for calculation, and then the result is adjusted by the BCD adjustment instruction, and the correct decimal operation result can be obtained. In fact, there are both adjustment instructions for combining the number of BCDs in the computer, and adjustment instructions for separating the number of BCDs. In addition, the addition and subtraction of the BCD code can also be converted into a binary number by the program before the operation, and then the binary number operation is processed by the computer, and the binary number result is converted from the program to the BCD code after the operation.
Convert hexadecimal numbers to 8421BCD encoding function.INCLUDE hardware.inc
.IRAM
_Led_Out:
.dw 0x0000, 0x0000, 0x0000, 0x0000, 0x0000, 0x0000, 0x0000, 0x0000
_List_8421_Data: //16 digits converted to 8421 code bit weight table, 10,000 bits per thousand carry, thousands per 100 carry, hundred for every ten carry
.dw 0xFFFF, 0xEA60, 0xC350, 0x9C40, 0x7530, 0x4E20, 0x2710
//60000-10000
.dw 0x2328,0x1F40,0x1B58,0x1770,0x1388,0x0FA0,0x0BB8,0x07D0,0x03E8
//9000-1000
.dw 0x0384,0x0320,0x02BC,0x0258,0x01F4,0x0190,0x012C,0x00C8,0x0064
//900-100
.dw 0x005A, 0x0050, 0x0046, 0x003C, 0x0032, 0x0028, 0x001E, 0x0014, 0x000A
//90-10
//.RAM
//.DATA
.code
//======================================================== ==================================================
/ / Function: hex_to_8421 ()
/ / Grammar: hex_to_8421 (converted number, symbol mark)
/ / Description: 16 digits converted to 8421 yards, stored in the array defined in the C segment
/ / Must define a subscript 8-bit integer array, the following paragraph C written
//extern int led_out [8]={0x0,0x0,0x0,0x0,0x0,0x0,0x0,0x0};
/ / Parameters: the number of converted to less than 0xFFFF, the symbol mark 0 or non-zero number
//Return: None
//======================================================== ======================================================
.PUBLIC _hex_to_8421;
_hex_to_8421: .PROC
Push bp to [sp];
Bp=sp+1; //Rebase address relocation, ready to take parameters
R1=[bp+3]; // Ready to convert to a 84-digit hexadecimal number
R3=[bp+4]; //signal bit flag, if 0, do unsigned integer processing, non-1 do signed number processing
R4=_Led_Out; //The address of the output data ***************************** can modify the output name
Bp=_List_8421_Data; //Base address is positioned to the bit table header ************************* corresponds to the .IRAM segment, the input name can be modified
//------------------------------------------
Test R3, 0xFFFF; / / check whether R3 is non-zero, if non-zero, do a signed number processing, if it is 0, do unsigned number processing
Je _hex_loop0; // is 0, do unsigned number processing, jump to _hex_loop0
R3=0xF000; //Non-zero, do signed number processing
[R4]=r3; //The first unit of the table is 4 bytes high and stores the symbol mark, F is negative, 0 is positive
R1-=0X0001; //includes the next step, after subtracting 1 and converting the inverse to a 10-digit positive number
R1^=0xFFFF;
_hex_loop0:
R2=0X0007; //R2 is the carry flag, from 9 to 1 cycle, R2 is initially set to 7, after entering the loop, minus 1 to 6 is the initial value.
//------------------------------------------
_hex_loop1: //Position table traversal start tag
CALL _Clear_WatchDog; // Clear watchdog
BP+=0X0001; //Base address plus 1, locate the first significant digit of the bit weight table
R2-=0X0001; //bit weight minus 1, prepare the bit number corresponding to the first significant digit of the output bit table
Cmp r1,[bp]; //Compare the number of converted numbers and the current bit weight
Jb _hex_loop2; //If the number of conversions is less than the current bit, skip to "_hex_loop1" and continue comparing
Jmp _hex_loop3; //If the number of conversions is greater than the current bit, skip to "_hex_loop3" and convert
_hex_loop2: //R2 carry loop processing tag
CMP R2, 0X0002;
JB _hex_loop4; //Includes the first step. If R2 is less than 2, jump to _hex_loop4 and set R2 to 10.
JMP _hex_loop1; //If R2 is greater than or equal to 2, skip to "_hex_loop1" and continue to compare
_hex_loop4:
R2=0x000A; //Include the next step, set R2 to 10, jump to "_hex_loop1", continue to compare
JMP _hex_loop1;
//------------------------------------------
_hex_loop3: //Mark and mark the output data
Cmp r1, 0x2710;
Jnb _hex_2710; //includes the first step. If R1 is greater than or equal to 0x2710(10000), skip to _hex_2710 to process
Cmp r1,0x03e8;
Jnb _hex_03e8; //Include the last step, if R1 is greater than or equal to 0x03E8 (1000), skip to _hex_03E8
Cmp r1, 0x0064;
Jnb _hex_0064; / / include the first step, if R1 is greater than or equal to 0x0064 (100), jump to _hex_0064 processing
Cmp r1,0x000a;
Jnb _hex_000a; //includes the first step. If R1 is greater than or equal to 0x000A(10), skip to _hex_000A for processing.
//------------------------------------------
R3=R4+5; //Include the next 2 steps, output the first digit of decimal, jump to “_hex_000â€, end the conversion
[R3]=R1;
Jmp _hex_over;
_hex_2710:
R3=R4+1; //Include the next 3 steps, output the 5th digit of the decimal digit, reduce the weight of the converted digit, do the converted number, jump to “_hex_loop1â€, continue to compare
[R3]=R2;
R1-=[bp];
Jmp _hex_loop1;
_hex_03e8:
R3=R4+2; //Include the next 3 steps, output the 4th digit of the decimal, the reduced number of the converted digits, do the converted number, jump to "_hex_loop1", continue to compare
[R3]=R2;
R1-=[bp];
Jmp _hex_loop1;
_hex_0064:
R3=R4+3; //Include the next 3 steps, output the 3rd digit of the decimal, the converted digits are subtracted, do the converted number, jump to “_hex_loop1â€, continue to compare
[R3]=R2;
R1-=[bp];
Jmp _hex_loop1;
_hex_000a:
R3=R4+4; //Include the next 3 steps, output the 2nd digit of the decimal, the reduced number of converted digits, do the converted number, jump to “_hex_loop1â€, continue to compare
[R3]=R2;
R1-=[bp];
Jmp _hex_loop1;
_hex_over:
Pop bp from [sp];
RETF
.ENDP;
.PUBLIC _Clear_WatchDog;
_Clear_WatchDog: .PROC
PUSH R1 TO [SP];
R1 = 0x0001;
[ASM_Port_Watchdog_Clear] = R1;
POP R1 FROM [SP];
RETF
.ENDP;
Dongguan Yijia Optoelectronics Co., Ltd. , https://www.everbestlcdlcm.com